a very fast algorithm for getting the circumcircle from a triangle - http://www.exaflop.org/docs/cgafaq/cga1.html#Subject 1.04

circumcircle.js

function circumcircle(a, b, c) {
  this.a = a
  this.b = b
  this.c = c

  var A = b.x - a.x,
      B = b.y - a.y,
      C = c.x - a.x,
      D = c.y - a.y,
      E = A * (a.x + b.x) + B * (a.y + b.y),
      F = C * (a.x + c.x) + D * (a.y + c.y),
      G = 2 * (A * (c.y - b.y) - B * (c.x - b.x)),
      minx, miny, dx, dy

  /* If the points of the triangle are collinear, then just find the
   * extremes and use the midpoint as the center of the circumcircle. */
  if(Math.abs(G) < 0.000001) {
    minx = Math.min(a.x, b.x, c.x)
    miny = Math.min(a.y, b.y, c.y)
    dx   = (Math.max(a.x, b.x, c.x) - minx) * 0.5
    dy   = (Math.max(a.y, b.y, c.y) - miny) * 0.5

    this.x = minx + dx
    this.y = miny + dy
    this.r = dx * dx + dy * dy
  }

  else {
    this.x = (D*E - B*F) / G
    this.y = (A*F - C*E) / G
    dx = this.x - a.x
    dy = this.y - a.y
    this.r = dx * dx + dy * dy
  }
}

@yahiko00
Checkmated

@louy @jimarlow Square root is "expensive" to compute. Having a squared distance is often enough.

Imagine you have a circle at (0,0) with a radius 5. Is the point (-4,4) inside that circle? You would probably test, if sqrt(16+16) < 5. Can you compute it without a calculator?

But actually, you can test, if 16+16 < 5*5, that is 32 < 25, which is not, so it is not in a circle. But it is in a circle of radius 6 (32<36).

Also, if the coordinates are integers, squared distances are also integers. You may not need to work with floats at all.

@louy @photopea Thank you guys, I don't even remember I ever wrote his.

I'd say it should be this, as it mentioned in the article:

this.rSq = dx * dx + dy * dy;

Since the reference page is gone, here is an archive link from the Wayback machine:
https://web.archive.org/web/20071030134248/http://www.exaflop.org/docs/cgafaq/cga1.html#Subject%201.01:%20How%20do%20I%20rotate%20a%202D%20point?

Depending on your circumstances you can do it with vectors. The intersection of at least two rays, each passing through the midpoint of a side of the triangle and perpendicular to that side, is the circumcenter. Proof seen here: https://flashman.neocities.org/Courses/Circumcenter.html

In this image below the (segments of) rays are M, N and P, each perpendicular to the side that they pass through the midpoint of:

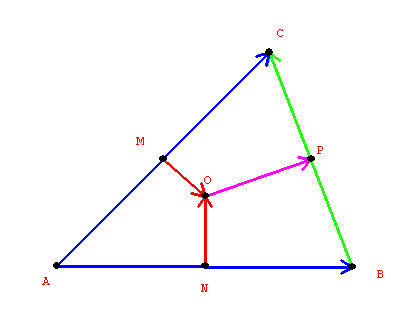
The circumcenter is O, equidistant to the 3 vertices. In some cases it can be outside of the triangle.