big-O_notation.md

Big-O Notation

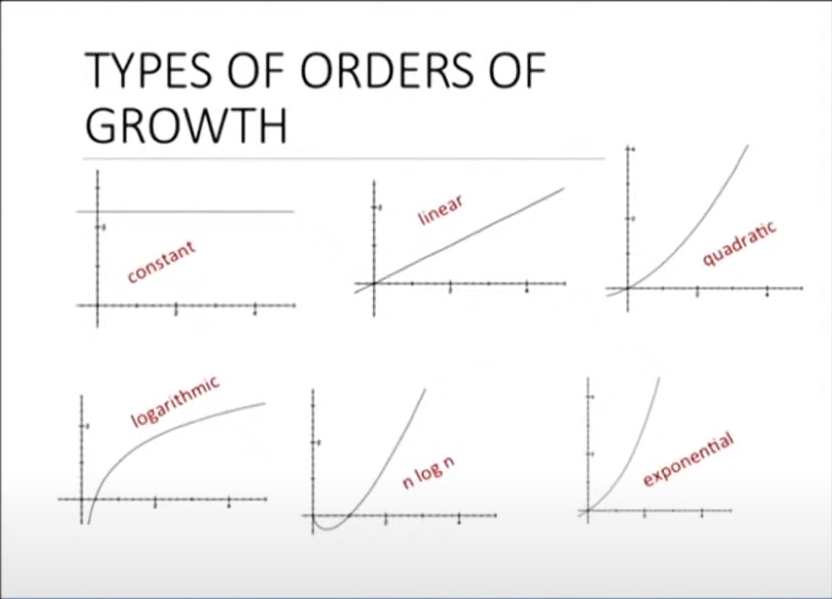
Função/notação matemática para descrever a ordem de grandeza/crescimento de um algoritmo conforme n (sendo n o parâmetro/tamanho da entrada).

O = Omicron

Análise assintótica / Matemática assintótica Uma analise uniforme/abstrata.

n^2

Regras para construir fórmula do big-O:

• Somar cada passo
• Ignore as contantes
• Ignore os fatores multiplicativos
• Ignore os fatores de menor crescimento

---

Análises de performance (Time space complexity)

Como a função escala no tempo de acordo com seus parametros de entrada.

Big-O sempre espera o pior cenário.

Tipos de equações de acordo com a ordem de crescimento:

1. Constante O(1)
2. Logarítmica O(log n)
3. Linear O(n)
4. Log-Linear O(n log n)
5. Quadrática O(n^2)
6. Exponencial O(2^n)

Eixo X = tamanho entrada - Eixo Y = tempo

Constante = O(1) / order n / O of n

Sempre vai levar o mesmo tempo independente do tamanho da entrada.
Exemplo de algoritmo:

"""
Celsius/Fahrenheit Calculator
"""
def c_to_f(c):
  return c*9.0/5 + 32

c_to_f(40)
# 104

Logarítmica = O(log n) na computação o log é sempre base 2.

Log por padrão se não é passado a base assume o valor 2.
Log 8 = x mesma coisa que 2 ^ x = 8

Exemplo de algoritmo:

"""
Bisect search - funciona em listas ordenadas, dividindo o problema sempre em partes menores.
"""
def bisect_search(L, e):
  def helper(L, e, low, high):
    if high == low:
      return L[low] == e

    mid = (low + high) // 2

    if L[mid] == e;
      return True
    elif L[mid] > e:
      if low == mid: #nothing left to search
        return False
      else:
        return helper(L, e, low, high - 1)
    else:
      return helper(L, e, mid + 1, high)

  if len(L) == 0:
    return False
  else:
    return helper(L, e, 0, len(L) -1)

L = [1,3,3,4,4,5,5,7,8,8,9,9,11,13,20]
bisect_search(L, 7)
# True

Linear = O(n)

Vai aumentando linearmente em função de n.
Exemplos de algoritmo:

"""
Fatorial
"""
def factorial(n):
  answer = 1
  while n > 1:
    answer *= n
    n -= 1
  return answer

factorial(5)
# 120

"""
Busca linear em uma lista não ordenada
"""
def linear_search(L, e):
  found = false
  for i in range(len(L)):
    if e == L[i]:
      found = True
  return found

L = [1,4,8,3,7,4,9,13,5,9,3]
linear_search(L, 10)
# False

Log-Linear = O(n log n)

Exemplo de algoritmo:

"""
Implementa o merge sort
"""
def merge_sort(L):
  def merge(left, right):
    result = []
    i,j = 0,0

    while i < len(left) and j < len(right):
      if left[i] < right[j]:
        result.append(left[i])
        i += 1
      else:
        result.append(right[j])
        j += 1
    
    while (i < len(left)):
      result.append(left[i])
      i += 1

    while (j < len(right)):
      result.append(right[j])
      j += 1
    
    return result

  if len(L) < 2:
    return L[:]
  else:
    middle = len(L)//2
    left = merge_sort(L[:middle])
    right = merge_sort(L[middle:])
    return merge(left, right)

L = [1,4,8,3,7,8,4,9,13,5,11,20,5,9,3,5,9,8,3,8,8,2,7,10,13,19,9]

merge_sort(L)
# 

Quadrática = O(n²)

Exemplo de algoritmo:

"""
Determina se uma lista é subset de outra.
"""
def is_subset(L1, L2):
  for e1 in L1:
    matched = False
    for e2 in L2:
      if e1 == e2:
        matched = True
        break
    
    if not matched:
      return False
  
  return True

L2 = [1,4,8,3,7,4,9,13,5,11,20]
L1 = [5,9,3]

is_subset(L1, L2)
# True

Exponencial = O(2n)

Exemplo de algoritmo:

"""
Gera o powerset de um determinado conjunto.
"""
def powerset(L1, L2):
  res = []
  if len(L) == 0:
    return [[]]
  
  smaller = powerset(L[:-1])
  extra = L[-1:]
  new = []

  for small in smaller:
    new.append(small + extra)
  
  return smaller + new

L = [1,3,5,7]

powerset(L)
# [
#   [],
#   [1],
#   [3],
#   [1,3],
#   [5],
#   [1,5],
#   [3,5],
#   [1,3,5],
#   [7],
#   [1,7],
#   [3,7],
#   [1,3,7],
#   [5,7],
#   [1,5,7],
#   [3,5,7],
#   [1,3,5,7]
# ]